# Attention mechanism  The attention mechanism[^1] was designed in 2014 to address the problem of fixed-length context vectors in the [[RNN encoder-decoder]] model. In the RNN Encoder-Decoder, the encoder compresses all the information of the input into the context vector. In contrast, the attention framework shifts part of the burden to the decoder: the encoder only has to *annotate* the input sequence and the decoder uses an *alignment model* to selectively retrieve the information it needs.  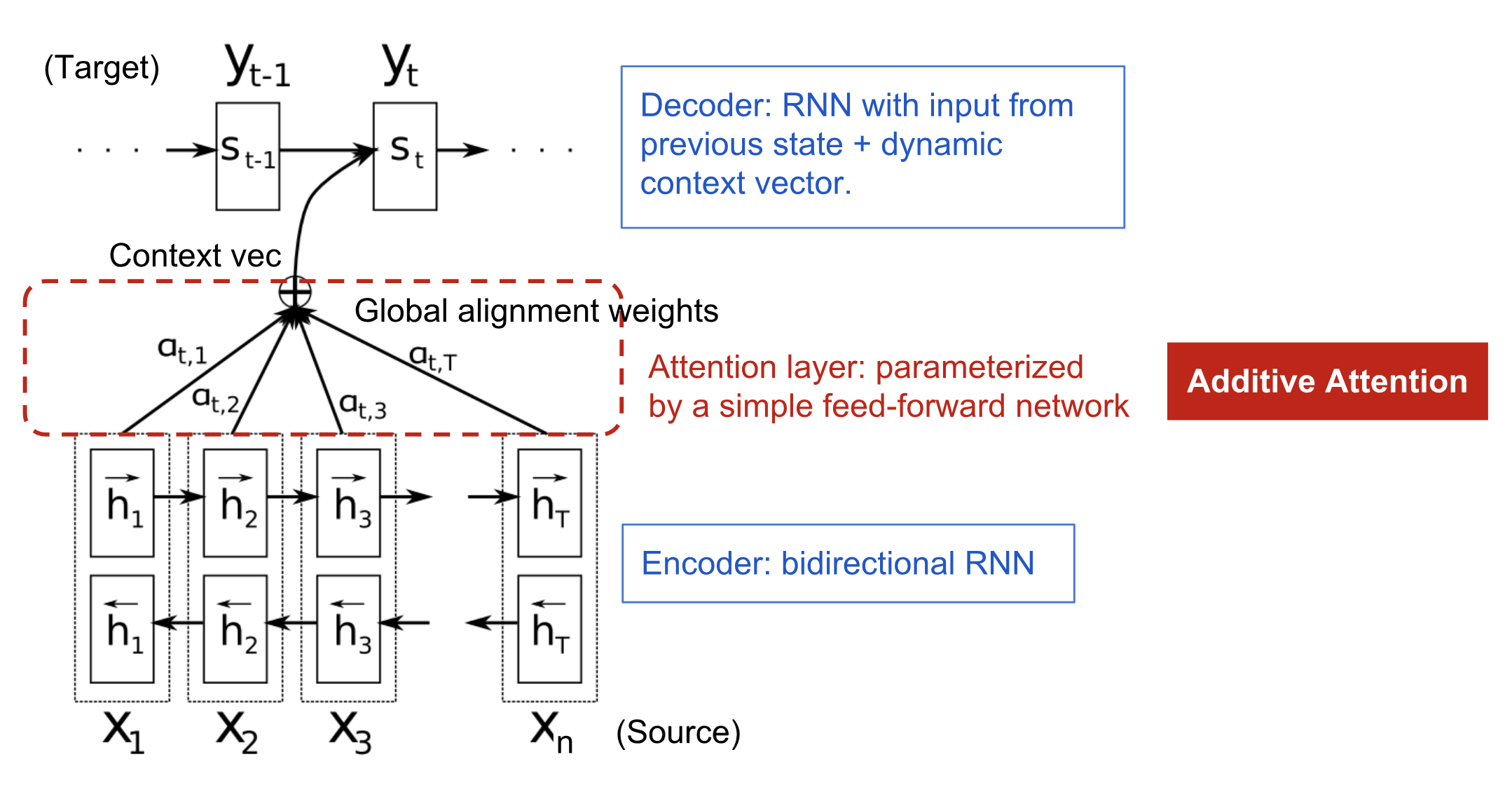## Encoder: bidirectional RNN for sequence annotation The encoder should annotate each word by summarizing both the preceding and following words, hence it is a bidirectional RNN. The forward RNN $\overrightarrow{f}$ reads the input sequence $(x_1, \dots, x_{T_x})$ from left to right and computes a sequence of *forward hidden states* $(\overrightarrow{h}_1, \dots, \overrightarrow{h}_{T_x})$; conversely, the backward RNN $\overleftarrow{f}$ reads the input from right to left and computes *backward hidden states* $(\overleftarrow{h}_1, \dots, \overleftarrow{h}_{T_x})$. The annotation $h_j$ for each word $x_j$ is obtained by concatenation of both hidden states: $ h_j = \left[ {\overrightarrow{h}_j}^\mathsf{T} \, ; \, {\overleftarrow{h}_j}^\mathsf{T} \right]^\mathsf{T} $ ## Decoder: RNN with alignment model for selective retrieval of information Each conditional probability for a word $y_i$ is defined as $ p(y_i \mid y_1, \dots, y_{i-1}, c_i) = g(y_{i-1}, s_i, c_i) $ where $g$ is a non-linear (potentially multi-layered) function and $s_i$ is the RNN hidden state for time $i$ computed by $ s_i = f(s_{i-1}, y_{i-1}, c_i) $ Unlike in the RNN Encoder-Decoder, there is a context vector $c_i$ for each word $y_i$. $c_i$ is computed as a weighted sum of the *annotations* $(h_1, \dots, h_{T_x})$ produced by the encoder: $ c_i = \sum_{j=1}^{T_x} \alpha_{ij} h_j \qquad \text{where} \qquad \alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^{T_x} \exp(e_{ik})} \qquad \text{where} \qquad e_{ij} = a(s_{i-1}, h_j) $ is an *alignment model* which scores how well the inputs around position $j$ and the output at position $i$ match. The score is based on the previous hidden state $s_{i-1}$ and the $j$-th annotation $h_j$ of the input. In the original paper by Bahdanau, $a$ is a feedforward neural network jointly trained with the rest of the architecture. Other alignment scores are possible, such as: - Content-base: $a(s_{i-1}, h_j) = \cos(s_{i-1}, h_j)$ - Location-base: $\alpha_{ij} = \mathrm{softmax}(\mathbf{W}_a s_{i-1})$ (no dependency on the source position) - General: $a(s_{i-1}, h_j) = s_{i-1}^\mathsf{T} \mathbf{W}_a h_j$ - Dot-product: $a(s_{i-1}, h_j) = s_{i-1}^\mathsf{T} h_j$ - Scaled dot-product: $a(s_{i-1}, h_j) = \frac{1}{\sqrt{n}} s_{i-1}^\mathsf{T} h_j$ (used in the [[Transformer model]]) ==The context vector $c_i$ can be understood as an *expected annotation*== with ==$\alpha_{ij}$ being the probability that $y_i$ is aligned with $x_j$==. Meanwhile, $\alpha_{ij}$ reflects the importance of the annotation $h_j$ with respect to the previous hidden state $s_{i-1}$ in deciding $s_i$ and generating $y_i$, ie, it reflects how much the decoder should pay *attention* to the annotation. ## Self-attention The [[Self-attention mechanism]] is a variation of the attention mechanism notoriously used in the [[Transformer model]]. --- ## 📚 References - Weng, Lilian. [“Attention? Attention!”](https://lilianweng.github.io/lil-log/2018/06/24/attention-attention.html) *Lil'Log*, 24 June 2018. - Olah, Chris, and Shan Carter. [“Attention and Augmented Recurrent Neural Networks.”](https://doi.org/10.23915/distill.00001) *Distill*, vol. 1, no. 9, Sept. 2016, p. e1. *distill.pub*, - Kosiorek, Adam. [_Attention in Neural Networks and How to Use It_.](https://akosiorek.github.io/ml/2017/10/14/visual-attention.html) - Karim, Raimi. [“Attn: Illustrated Attention.”](https://towardsdatascience.com/attn-illustrated-attention-5ec4ad276ee3) Medium, 1 Mar. 2020. - Luong, Minh-Thang, et al. [“Effective Approaches to Attention-Based Neural Machine Translation.”](http://arxiv.org/abs/1508.04025) ArXiv:1508.04025 [Cs], Sept. 2015. arXiv.org. [^1]: Bahdanau, Dzmitry, et al. [“Neural Machine Translation by Jointly Learning to Align and Translate.”](http://arxiv.org/abs/1409.0473) *ArXiv:1409.0473 [Cs, Stat]*, May 2016.