# Expectation-maximisation algorithm The expectation-maximisation algorithm is an iterative method used to find maximum likelihood estimates of parameters in statistical models which depend on unobserved latent variables. It alternates between an expectation (E) step and a maximisation (M) step. ## Setting Let $\mathbf{X}$ be a set of observed data, $\mathbf{Z}$ a set of unobserved latent data and $\boldsymbol{\theta}$ a vector of unknown parameters which characterize the distributions of $\mathbf{X}$ and $\mathbf{Z}$ through a likelihood function : $ L(\boldsymbol{\theta}; \mathbf{X}, \mathbf{Z}) \coloneqq p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol{\theta}) $ We want to find $\arg\max_\boldsymbol{\theta} L(\boldsymbol{\theta}; \mathbf{X})$. For instance, $\mathbf{X}$ could be a set of points, $\mathbf{Z}$ their masked colours (red or blue) and $\boldsymbol{\theta}$ the parameters of the red and blue probability distributions. ## E step We compute $Q(\boldsymbol{\theta}, \boldsymbol{\theta}_t) \coloneqq \mathbb{E}_{\mathbf{Z} \mid \mathbf{X}, \boldsymbol{\theta}_t} [\log L(\boldsymbol{\theta};\mathbf{X},\mathbf{Z})]$ the expected value of the log-likelihood function of $\boldsymbol{\theta}$ w.r.t. the current conditional distribution of $\mathbf{Z}$ given $\mathbf{X}$ and the current estimate $\boldsymbol{\theta}_t$. This amounts to expressing an estimate of $\mathbf{Z}$ given $\mathbf{X}$ and $\boldsymbol{\theta}_t$ as a function of $\boldsymbol{\theta}$ ; for instance, expressing the probability of a data point being of colour red given our current estimates. ## M step Here we compute $\boldsymbol{\theta}_{t+1} = \arg \max_\boldsymbol{\theta} Q(\boldsymbol{\theta} \mid \boldsymbol{\theta}_t)$ , either analytically or through optimisation models ; for instance, the best parameters for the red and blue distributions of data points, given our expected values of their colours $\mathbf{Z}$. 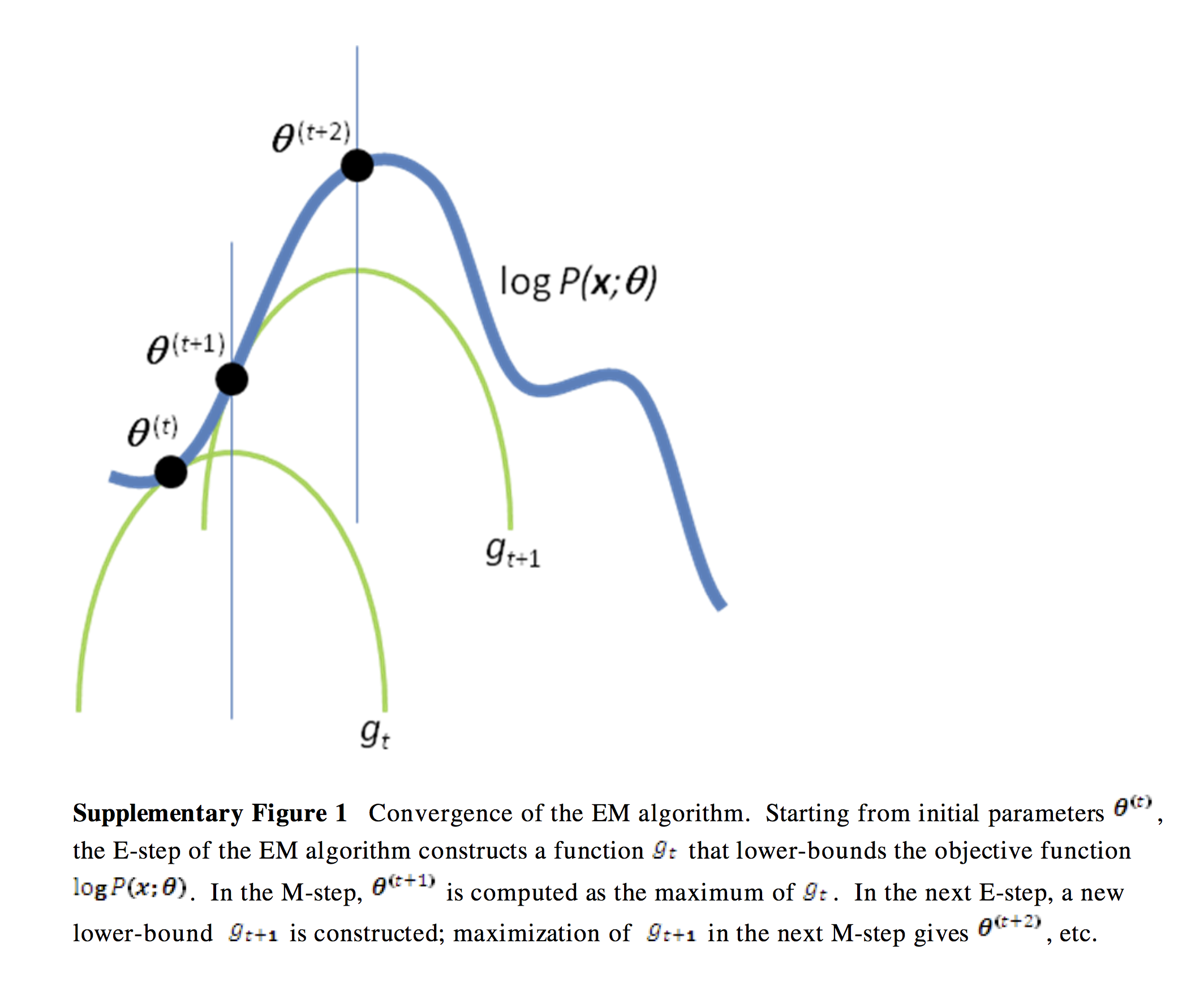## Visualisation