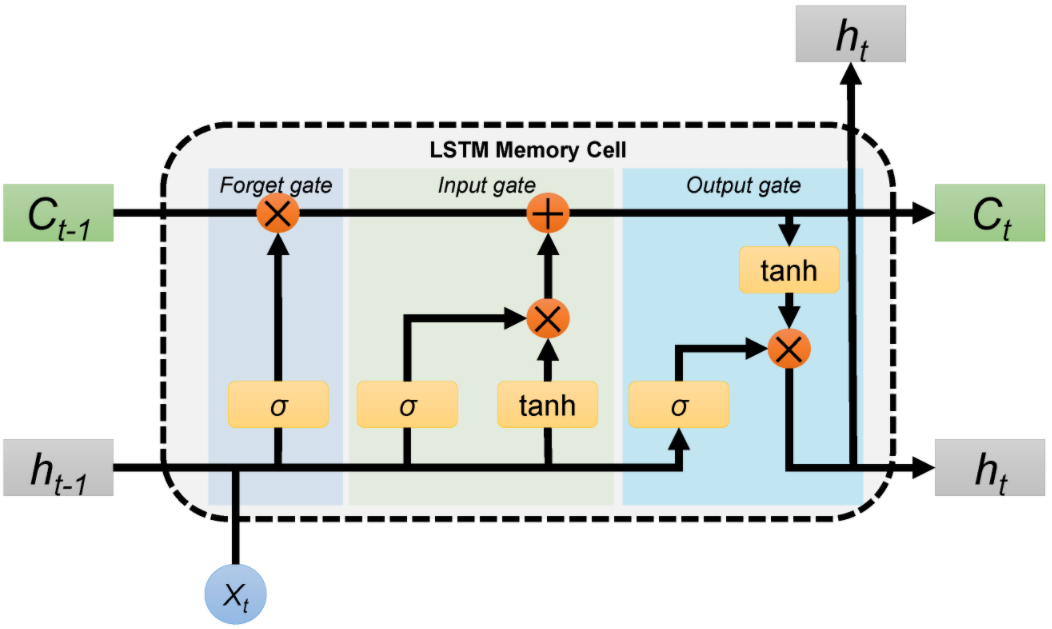
# Long short-term memory The long short-term memory (LSTM) unit is composed of a cell, an input gate, an output gate and a forget gate. They are well-suited to processing time series data because they were developed to deal with the vanishing gradient problem and are thus relatively insensitive to gap length, contrary to RNNs.  - $f_t = \sigma (W_f \cdot [h_{t-1}, x_t] + b_f)$ is the forget gate (first sigmoid) - $i_t = \sigma (W_i \cdot [h_{t-1}, x_t] + b_i)$ is the input gate (second sigmoid) - $\tilde{C}_t = \tanh (W_C \cdot [h_{t-1}, x_t] + b_C)$ is the cell input activation - $C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$ is the new cell state - $o_t = \sigma (W_o \cdot [h_{t-1}, x_t] + b_o)$ is the output gate (third sigmoid) - $h_t = o_t \odot \tanh (C_t)$ is the new hidden state All this terminology looks quite impressive, but the intuition behind is straightforward. The core idea of the LSTM is to propagate a cell state along the time dimension, while updating it along the way. The previous cell state $C_{t-1}$ is multiplied by the forget gate $f_t \in [0,1]$, and the cell input activation $\tilde{C}_t$ is multiplied by the input gate $i_t \in [0,1]$. The new cell state $C_t$ is simply the sum of both. Then, the output is $\tanh(C_t)$ multiplied by the output gate $o_t \in [0,1]$. ## Variants ### Peephole LSTM  Here, the gates can look at the cell state. Some peepholes can be omitted. ### Coupled forget and input gates  Here, we only forget when we update the cell state. ### Gated recurrent unit See [[Gated recurrent unit]]. --- ## 📚 References - Hochreiter, Sepp and Jürgen Schmidhuber. ["Long Short-term Memory."](https://doi.org/10.1162/neco.1997.9.8.1735) Neural Comput., vol. 9, no. 8, 1 Dec. 1997, pp. 1735-80. - ["Understanding LSTM Networks -- colah's blog."](https://colah.github.io/posts/2015-08-Understanding-LSTMs) 27 August 2015. - ["Long short-term memory | Wikipedia."](https://en.wikipedia.org/wiki/Long_short-term_memory) Wikipedia, 21 Sept. 2021.