> Wolfe, Cameron R. 'Mixture-of-Experts (MoE) LLMs'. _Deep (Learning) Focus_, 27 Jan. 2025, [https://cameronrwolfe.substack.com/p/moe-llms](https://cameronrwolfe.substack.com/p/moe-llms). # Mixture-of-Experts (MoE) LLMs - For the basic principles of MoE LLMs, see [[@wolfeMixtureExpertsMoEBirth2024|Mixture-of-Experts (MoE): The Birth and Rise of Conditional Computation]]. - Here, we discuss techincal details of MoE implementations, such as the auxiliary loss-functions used in MoE models. ## Importance Loss - To encourage a balanced selection of experts during training, we can simply add an additional constraint to the training loss that rewards the model for uniformly leveraging each of its experts. - This can be done by defining an "importance" score for each expert. The importance score is based upon the probability predicted for each expert by the routing mechanism. - Given a batch of data, we compute importance by taking a sum of the probabilities assigned to each expert across all tokens in the batch. - Then, to determine if these probabilities are balanced, we can take the squared [coefficient of variation (CV)](https://en.wikipedia.org/wiki/Coefficient_of_variation) of the expert importance scores. - Put simply, **the CV will be a small value if all experts have similar importance scores and vice versa**.  ## Load Balancing - Although the importance loss described above is useful, just because experts are assigned equal importance does not mean that tokens are routed uniformly. - For example, experts would have equal importance with: - A few tokens that assign them very high probability; - A much larger number of tokens that assign lower probability. 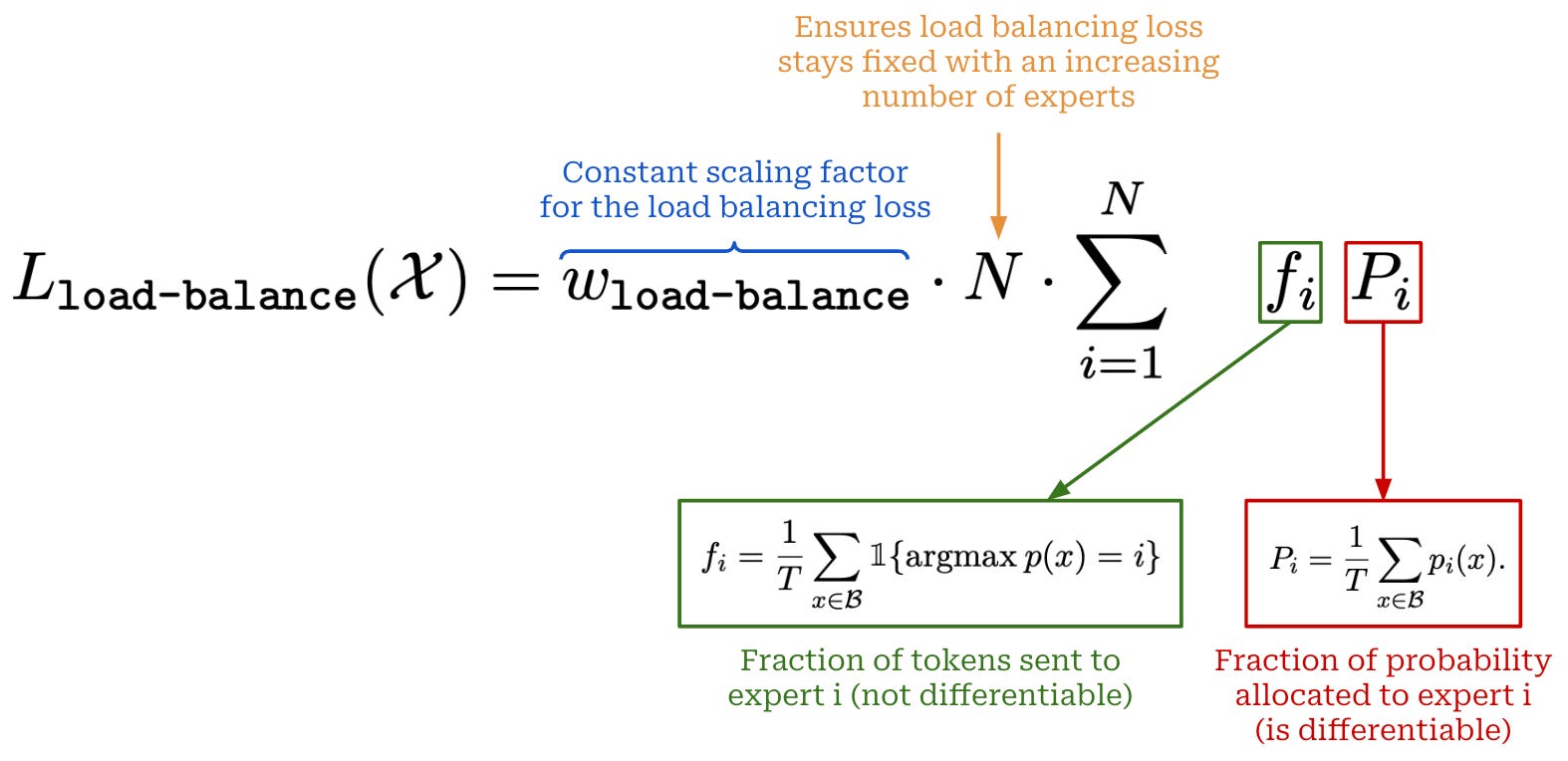- To solve this problem, we can create a single auxiliary loss term that captures both expert importance and load balancing, defined as the equal routing of tokens between each of the experts. This loss usually considers two quantities: 1. The fraction of router probability allocated to each expert; 2. The fraction of tokens dispatched to each expert.  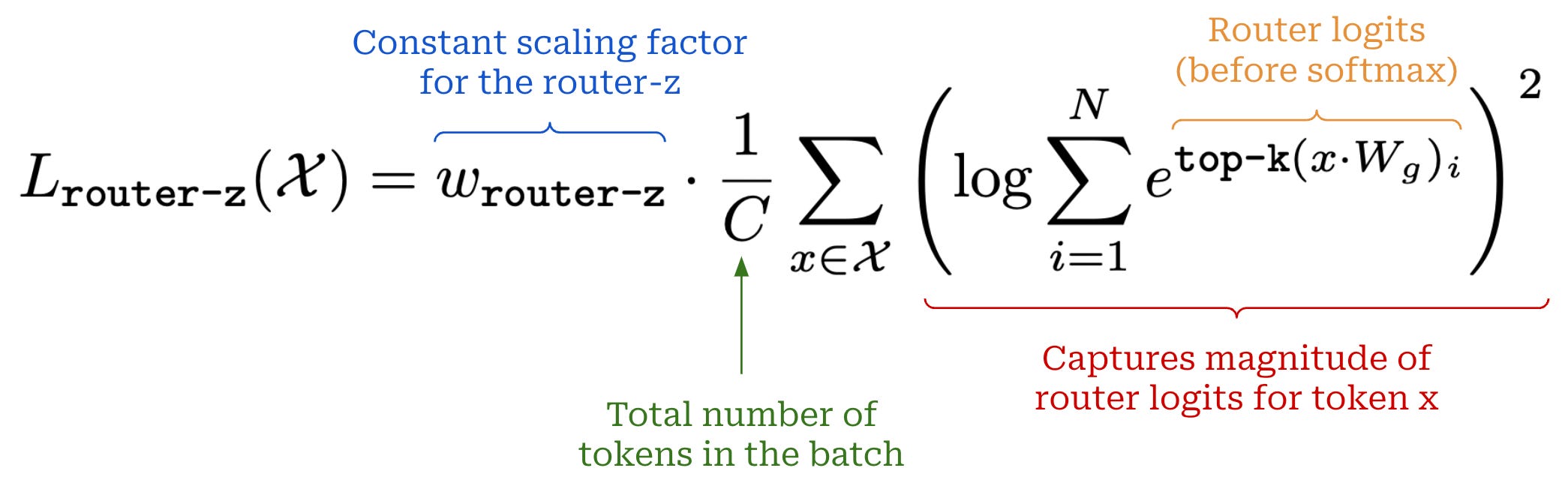## Router $z$-loss - The auxiliary load balancing loss described above is widely used throughout the MoE literature, but some authors propose an extra auxiliary loss term, called the **router $z$-loss**, that can further improve training stability. - The router z-loss constrains the size of the logits—**not the probabilities, so this is before softmax is applied**—predicted by the routing mechanism.  ## Expert Capacity - The computation performed in an MoE layer is dynamic due to the routing decisions made during both training and inference. - However, when we look at most practical implementations of sparse models, we will see that **==they usually have static batch sizes==**—**this is a useful trick for improving hardware utilization**. - To formalize the fixed batch size that we set for each expert, we can define the **expert capacity**: $ \textrm{Expert Capacity} \coloneqq \frac{\textrm{Total Batch Tokens}}{N} \cdot \textrm{Capacity Factor} $ - The expert capacity defines the maximum number of tokens in a batch that can be sent to each expert. - If the number of tokens routed to an expert exceeds the expert capacity, then we just "drop" these extra tokens. - More specifically, we perform no computation for these tokens and let their representation flow directly to the next layer via the transformer's residual connection.  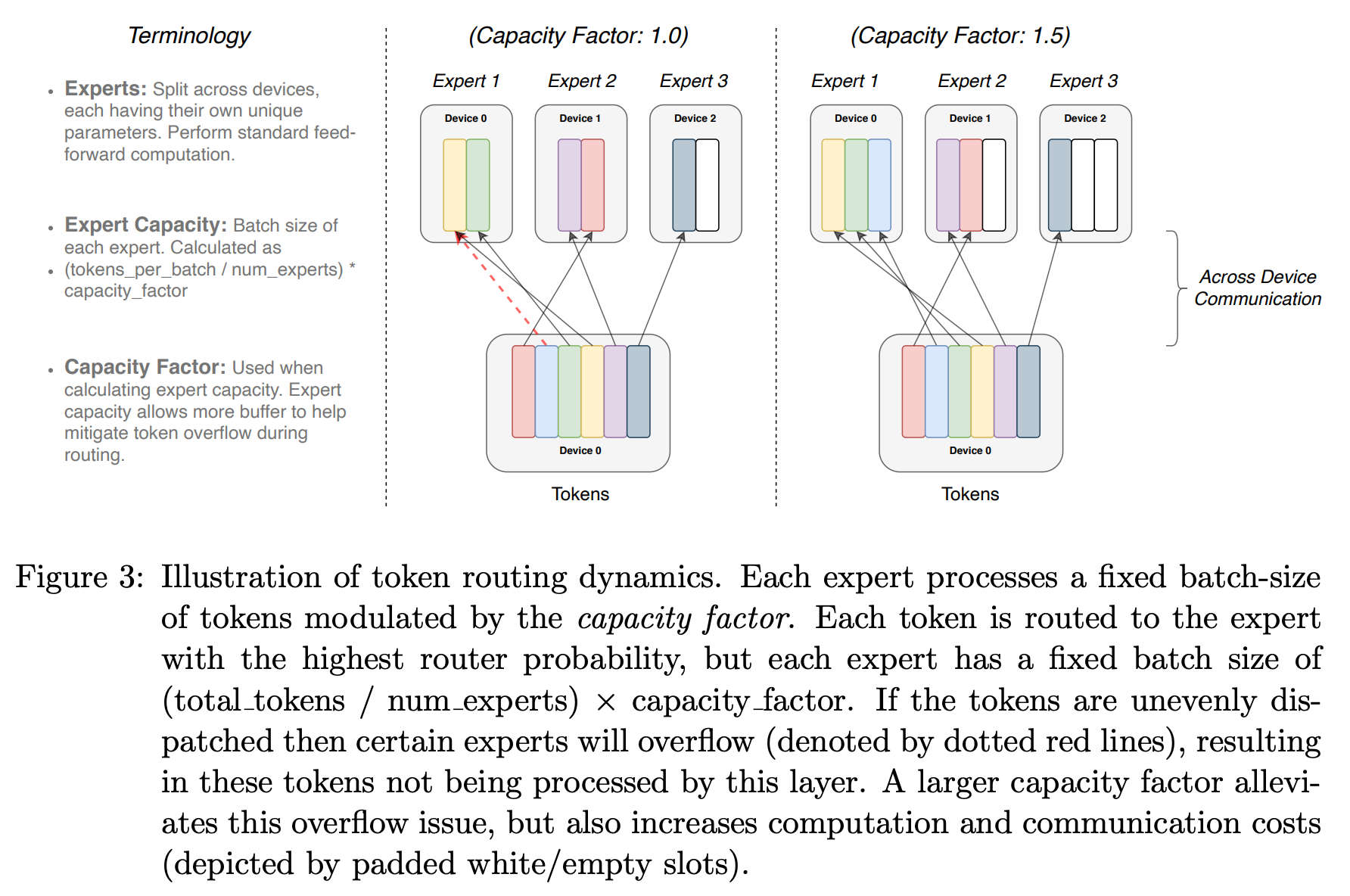- Interestingly, **MoE models tend to perform well with relatively low capacity factors (between 1 and 2)**. 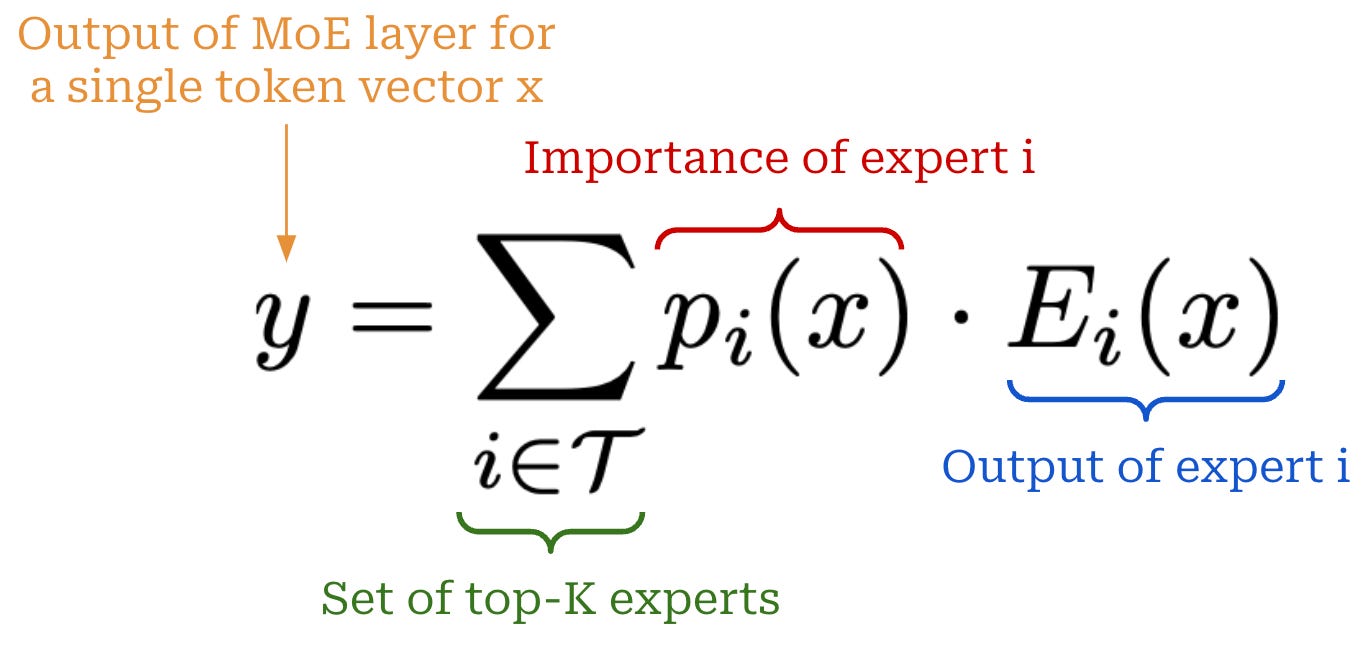## Computing the Output 1. Send the tokens to their selected experts. 2. Compute the output of the experts for these tokens. 3. Take a weighted average of expert outputs, where the weights are simply the probabilities assigned to each expert by the router.  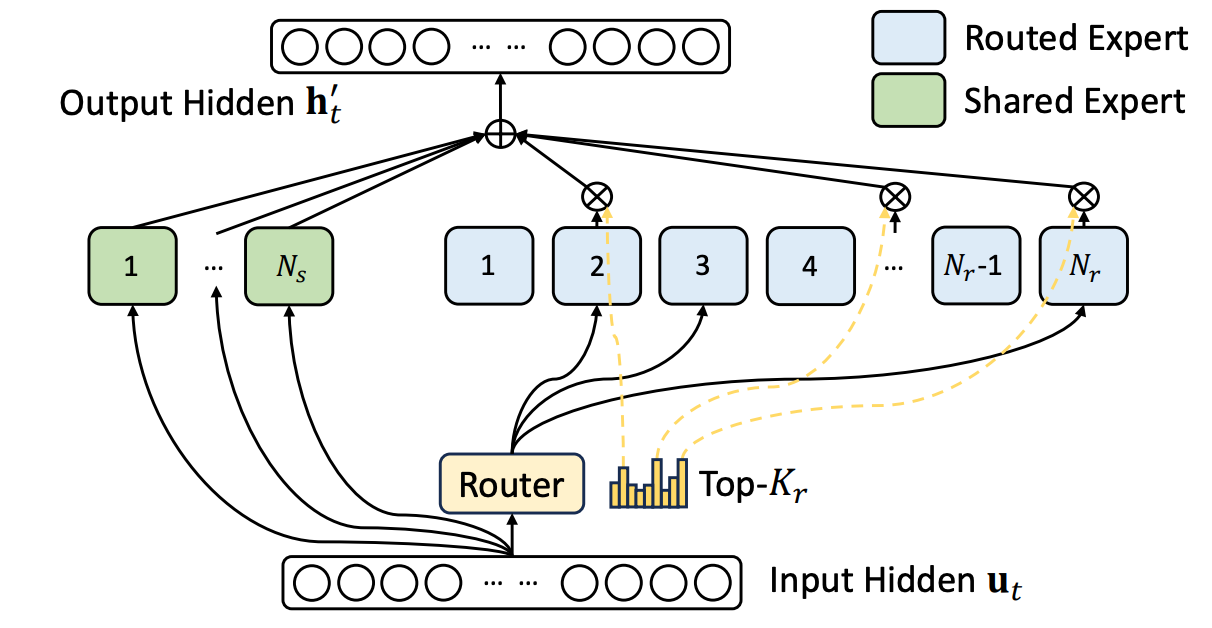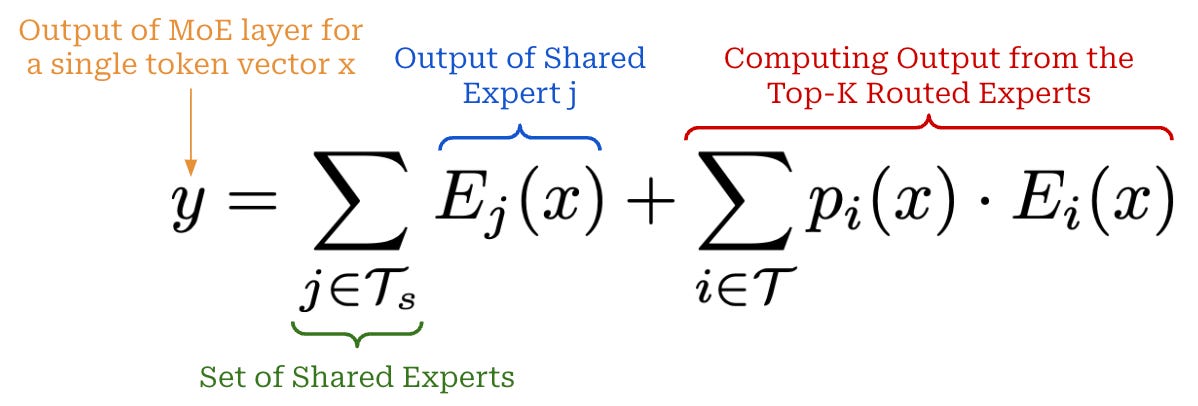## Shared Experts - We have two groups of experts—**shared experts and routed experts**. - All tokens are always passed through the shared experts. - Tokens are passed through the routed experts according to a normal MoE routing mechanism. - Usually, the number of shared experts must be lower than the number of routed experts—**increasing the number of shared experts degrades the sparsity benefits of the MoE**. - ==**The motivation behind using shared experts is minimizing the amount of redundant information between experts.**== - By having a set of shared experts, **we can allow the network to store shared information within these experts**, rather than having to replicate the same information across several different experts.   ## MoE Language Models - DeepSeek-AI, et al. _DeepSeek-V3 Technical Report_. arXiv:2412.19437, arXiv, 18 Feb. 2025. _arXiv.org_, [https://doi.org/10.48550/arXiv.2412.19437](https://doi.org/10.48550/arXiv.2412.19437). - DeepSeek-AI, et al. _DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model_. arXiv:2405.04434, arXiv, 19 June 2024. _arXiv.org_, [https://doi.org/10.48550/arXiv.2405.04434](https://doi.org/10.48550/arXiv.2405.04434). - 'Introducing DBRX: A New State-of-the-Art Open LLM'. _Databricks_, 27 Mar. 2024, [https://www.databricks.com/blog/introducing-dbrx-new-state-art-open-llm](https://www.databricks.com/blog/introducing-dbrx-new-state-art-open-llm). - Xue, Fuzhao, et al. _OpenMoE: An Early Effort on Open Mixture-of-Experts Language Models_. arXiv:2402.01739, arXiv, 27 Mar. 2024. _arXiv.org_, [https://doi.org/10.48550/arXiv.2402.01739](https://doi.org/10.48550/arXiv.2402.01739). - _Open Release of Grok-1 | xAI_. 17 Mar. 2024, [https://x.ai/news/grok-os](https://x.ai/news/grok-os). - Jiang, Albert Q., et al. _Mixtral of Experts_. arXiv:2401.04088, arXiv, 8 Jan. 2024. _arXiv.org_, [https://doi.org/10.48550/arXiv.2401.04088](https://doi.org/10.48550/arXiv.2401.04088).